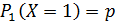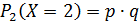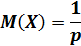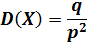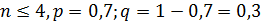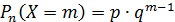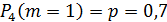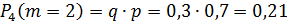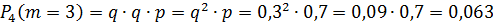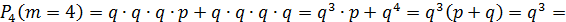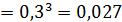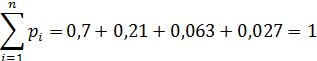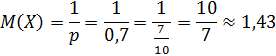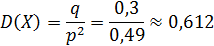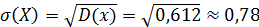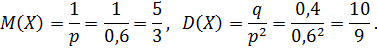Дискретная случайная величина: примеры решений задач

На этой странице мы собрали примеры решения учебных задач о дискретных случайных величинах. Это довольно обширный раздел: изучаются разные законы распределения (биномиальный, геометрический, гипергеометрический, Пуассона и другие), свойства и числовые характеристики, для каждого ряда распределения можно строить графические представления: полигон (многоугольник) вероятностей, функцию распределения.

Ниже вы найдете примеры решений о дискретных случайных величинах, в которых требуется применить знания из предыдущих разделов теории вероятностей для составления закона распределения, а затем вычислить математическое ожидание, дисперсию, среднее квадратическое отклонение, построить функцию распределения, дать ответы на вопросы о ДСВ и т.п.

Примеры для популярных законов распределения вероятностей:

Калькуляторы на характеристики ДСВ

Решенные задачи о ДСВ

Распределения, близкие к геометрическому

Задача 1. На пути движения автомашины 4 светофора, каждый из которых запрещает дальнейшее движение автомашины с вероятностью 0,5. Найти ряд распределения числа светофоров, пройденных машиной до первой остановки. Чему равны математическое ожидание и дисперсия этой случайной величины?

Задача 2. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. Найти дисперсию этой случайной величины.

Задача 3. Стрелок, имея 3 патрона, стреляет в цель до первого попадания. Вероятности попадания при первом, втором и третьем выстрелах соответственно 0,6, 0,5, 0,4. С.В. $\xi$ — число оставшихся патронов. Составить ряд распределения случайной величины, найти математическое ожидание, дисперсию, среднее квадратичное отклонение с.в., построить функцию распределения с.в., найти $P(|\xi-m| \le \sigma$.

Задача 4. В ящике содержится 7 стандартных и 3 бракованных детали. Вынимают детали последовательно до появления стандартной, не возвращая их обратно. $\xi$ — число извлеченных бракованных деталей.
Составить закон распределения дискретной случайной величины $\xi$, вычислить ее математическое ожидание, дисперсию, среднее квадратическое отклонение, начертить многоугольник распределения и график функции распределения.

Задачи с независимыми событиями

Задача 5. На переэкзаменовку по теории вероятностей явились 3 студента. Вероятность того, что первый сдаст экзамен, равна 0,8, второй — 0,7, третий — 0,9. Найдите ряд распределения случайной величины $\xi$ числа студентов, сдавших экзамен, постройте график функции распределения, найдите $М(\xi), D(\xi)$.

Задача 6. Вероятность попадания в цель при одном выстреле равна 0,8 и уменьшается с каждым выстрелом на 0,1. Составить закон распределения числа попаданий в цель, если сделано три выстрела. Найти математическое ожидание, дисперсию и С.К.О. этой случайной величины. Построить график функции распределения.

Задача 7. По цели производится 4 выстрела. Вероятность попадания при этом растет так: 0,2, 0,4, 0,6, 0,7. Найти закон распределения случайной величины $X$ — числа попаданий. Найти вероятность того, что $X \ge 1$.

Задача 8. Подбрасываются две симметричные монеты, подсчитывается число гербов на обеих верхних сторонах монет. Рассматривается дискретная случайная величина $X$- число выпадений гербов на обеих монетах. Записать закон распределения случайной величины $X$, найти ее математическое ожидание.

Другие задачи и законы распределения ДСВ

Задача 9. Два баскетболиста делают по три броска в корзину. Вероятность попадания для первого баскетболиста равна 0,6, для второго – 0,7. Пусть $X$ — разность между числом удачных бросков первого и второго баскетболистов. Найти ряд распределения, моду и функцию распределения случайной величины $X$. Построить многоугольник распределения и график функции распределения. Вычислить математическое ожидание, дисперсию и среднее квадратичное отклонение. Найти вероятность события $(-2 \lt X \le 1)$.

Задача 10. Число иногородних судов, прибывающих ежедневно под погрузку в определенный порт – случайная величина $X$, заданная так:
0 1 2 3 4 5
0,1 0,2 0,4 0,1 0,1 0,1
А) убедитесь, что задан ряд распределения,
Б) найдите функцию распределения случайной величины $X$,
В) если в заданный день прибывает больше трех судов, то порт берет на себя ответственность за издержки вследствие необходимости нанимать дополнительных водителей и грузчиков. Чему равна вероятность того, что порт понесет дополнительные расходы?
Г) найдите математическое ожидание, дисперсию и среднее квадратическое отклонение случайной величины $X$.

Задача 11. Бросают 4 игральные кости. Найти математическое ожидание суммы числа очков, которые выпадут на всех гранях.

Задача 12. Двое поочередно бросают монету до первого появления герба. Игрок, у которого выпал герб, получает от другого игрока 1 рубль. Найти математическое ожидание выигрыша каждого игрока.

Решебник по терверу

Нужны еще решения? Найди в решебнике свое (от 30 рублей и мгновенная доставка):

Геометрический закон распределения (геометрическое распределение) дискретных случайных величин.

Дискретная случайная величина распределена геометрически, если она принимает значения 1,2,…m …(бесконечное, но счетное количество раз) с вероятностями, находящимися по формуле общего члена геометрической прогрессии:

Случайная величина X = m, распределенная геометрически, представляет собой число испытаний (m) до первого положительного исхода.

Составим ряд распределения:

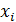	…	m	…
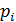	p		…		…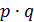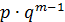

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной геометрически, вычисляются по формулам:

Пример.

Охотник стреляет по дичи до первого попадания, но успевает сделать не более 4‒х выстрелов.

Составить закон распределения числа выстрелов, если вероятность попадания при одном выстреле равна p = 0,7.

Решение:

число выстрелов

Составим закон распределения числа выстрелов:

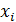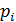	0,7	0,21	0,063	0,027

Проверка:

1. Математическое ожидание:

3. Среднее квадратическое откланение:

4. так как при m = 1 вероятность максимальная, она составляет

Пример.

Вероятность поражения цели равна 0,6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.

Решение:

Случайная величина X — число сделанных выстрелов — имеет геометрическое распределение с параметром p=0,6. Ряд распределения X имеет вид:

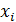	.	m	.
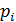	0,6	0,24	0,096	.	0,6·0,4m	.

Вероятность того, что для поражения цели потребуется не более трёх патронов равнаP(X≤3) = P(X=1) + P(X=2) + P(X=3) = 0,6+0,24+0,096 = 0,936.

Охотник стреляет по дичи до первого попадания, но успевает делать не более четырёх выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

Готовое решение: Заказ №8392

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 30.09.2020

Цена: 118 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Охотник стреляет по дичи до первого попадания, но успевает делать не более четырёх выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

Решение.

Вероятность попадания в цель при одном выстреле равна p = 0,7. Тогда вероятность промаха q = 1 – p = 1 – 0,7 = 0,3. Случайная величина Х – число промахов – может принимать значения 0, 1, 2, 3 или 4.

Найдём вероятности значений случайной величины Х.

Будет 0 промахов, если охотник попадёт первым же выстрелом: .

Будет 1 промах, если охотник попадёт вторым выстрелом: .

Будет 2 промаха, если охотник попадёт третьим выстрелом: .

Будет 3 промаха, если охотник попадёт четвёртым выстрелом:

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназачен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. составить закон распределения числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7. найти среднее число попаданий при этих условиях.

Ответы

РЕШЕНИЕ. 1 задача

Введем дискретную случайную величину X = (Число промахов). X может принимать

значения 0, 1, 2, 3, 4

Найдем соответствующие вероятности.

X = 0 , если охотник попал в дичь при первом выстреле, поэтому P(X = 0) = 0,7 .

X =1 , если охотник не попал в дичь при первом выстреле и попал в дичь при втором

выстреле, поэтому P(X =1) = 0,3 ⋅0,7 = 0,21.

X = 2 , если охотник не попал в дичь при первом выстреле и втором выстреле, и попал в

дичь при третьем выстреле, поэтому P(X = 2) = 0,3 ⋅0,3 ⋅0,7 = 0,063 .

X = 3, если охотник не попал в дичь при первом, втором и третьем выстреле, и попал в

дичь при четвертом выстреле, поэтому P(X = 3) = 0,3⋅0,3 ⋅0,3 ⋅0,7 = 0,0189 .

X = 4 , если охотник не попал в дичь при первом, втором, третьем и четвертом выстрелах,

поэтому P(X = 4) = 0,3 ⋅0,3 ⋅0,3 ⋅0,3 = 0,0081.

Закон распределения X :

Найдем числовые характеристики с.в. X .

M ( X ) =∑ xi pi = 0 ⋅0,7 +1⋅0,21+ 2 ⋅0,063+ 3⋅0,0189 + 4 ⋅0,0081 = 0,4251.

x2=∑ i pi −(M ( X ))2 =0⋅0,7+1⋅0,21+4⋅0,063+9⋅0,0189+16 ⋅0,0081−0,4251 ≈0,581.

Х может принимать значения 0,1,2,3,4,5,6

Вероятности ищи по формуле

Р (0)=q=0,5 — остановился перед первым же светофором

Р (1)=q*р=0,5*0,5 — первый остановился перед вторым

Р (2)=0,5*0,5^2 -2 первых остановился перед 3м

Р (6)=р все 6 светофоров без остановки

Х число промахов =(0,1,2,3,4)

Вероятность попадания с 1-го раза и использования только 1 патрона — 0,6.

Чтобы использовать 2-й патрон нужно не попасть с 1-го раза (вероятность 1-0,6 = 0,4) и попасть со 2-го раза (вероятность 0,6). Вероятность такого события 0,4*0,6 = 0,24.

Для использования 3-го патрона нужно не попасть 1-й раз (вероятность 0,4), не попасть 2-й раз (вероятность 0,4) и попасть 3- раз (вероятность 0,6). Вероятность использования 3 патрона 0,4*0,4*0,6 = 0,096.

Аналогично вычисляем вероятность того, что стрелок попадёт в мишень с 4-го раза: 0,4*0,4*0,4*0,6 = 0,0384.

Осталось вычислить вероятность того, что ни один патрон не попадёт в цель: 0,4*0,4*0,4*0,4 = 0,0256.

Использование 4 патронов возможно в 2-х несовместимых случаях: стрелок попадёт в мишень с 4-го раза или 4 раза промахнётся, поэтому вероятность такого события 0,0384+0,0256 = 0,064

Запишем закон распределения СВ в виде таблицы: Х__|___1___|___2___|___3___|___4___| P__|__.0,6__|_.0,24__|_.0,096_|__0,064_|