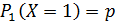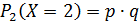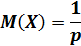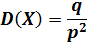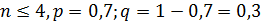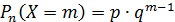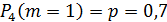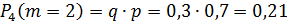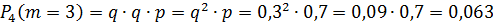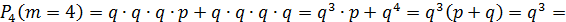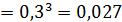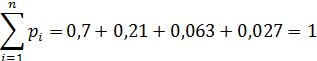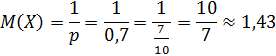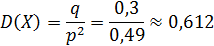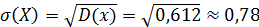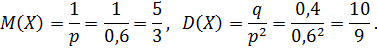Геометрический закон распределения (геометрическое распределение) дискретных случайных величин.

Дискретная случайная величина распределена геометрически, если она принимает значения 1,2,…m …(бесконечное, но счетное количество раз) с вероятностями, находящимися по формуле общего члена геометрической прогрессии:

Случайная величина X = m, распределенная геометрически, представляет собой число испытаний (m) до первого положительного исхода.

Составим ряд распределения:

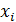	…	m	…
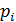	p		…		…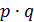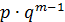

Теорема. Математическое ожидание и дисперсия случайной величины, распределенной геометрически, вычисляются по формулам:

Пример.

Охотник стреляет по дичи до первого попадания, но успевает сделать не более 4‒х выстрелов.

Составить закон распределения числа выстрелов, если вероятность попадания при одном выстреле равна p = 0,7.

Решение:

число выстрелов

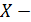
Составим закон распределения числа выстрелов:

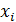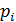	0,7	0,21	0,063	0,027

Проверка:

1. Математическое ожидание:

3. Среднее квадратическое откланение:

4. так как при m = 1 вероятность максимальная, она составляет

Пример.

Вероятность поражения цели равна 0,6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.

Решение:

Случайная величина X — число сделанных выстрелов — имеет геометрическое распределение с параметром p=0,6. Ряд распределения X имеет вид:

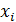	.	m	.
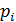	0,6	0,24	0,096	.	0,6·0,4m	.

Вероятность того, что для поражения цели потребуется не более трёх патронов равнаP(X≤3) = P(X=1) + P(X=2) + P(X=3) = 0,6+0,24+0,096 = 0,936.

Охотник стреляет по дичи до первого попадания, но успевает делать не более четырёх выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

Готовое решение: Заказ №8392

Тип работы: Задача

Статус: Выполнен (Зачтена преподавателем ВУЗа)

Предмет: Теория вероятности

Дата выполнения: 30.09.2020

Цена: 118 руб.

Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.

Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!

Описание и исходные данные задания, 50% решения + фотография:

Охотник стреляет по дичи до первого попадания, но успевает делать не более четырёх выстрелов. Найти дисперсию числа промахов, если вероятность попадания в цель при одном выстреле равна 0,7.

Решение.

Вероятность попадания в цель при одном выстреле равна p = 0,7. Тогда вероятность промаха q = 1 – p = 1 – 0,7 = 0,3. Случайная величина Х – число промахов – может принимать значения 0, 1, 2, 3 или 4.

Найдём вероятности значений случайной величины Х.

Будет 0 промахов, если охотник попадёт первым же выстрелом: .

Будет 1 промах, если охотник попадёт вторым выстрелом: .

Будет 2 промаха, если охотник попадёт третьим выстрелом: .

Будет 3 промаха, если охотник попадёт четвёртым выстрелом:

Присылайте задания в любое время дня и ночи в whatsapp.

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназачен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Сайт о компьютерной технике

Охотник стреляет по дичи до первого попадания. Теория вероятностей и математическая статистика. По условию задачи имеем

Задание 5.

Условие: Прибор может собираться из деталей высокого качества и деталей обычного качества. Из высококачественных деталей собирается 40 % приборов.

Для высококачественного прибора его надежность за промежуток времени t равна 0.95, для обычных приборов надежность составляет 0.7. Прибор испытывался в течение времени t и работал безотказно.

Найти вероятность того, что он собран из высококачественных деталей.

Решение : Н 1 — прибор собран из высококачественных деталей,

Н 2 — прибор собран из деталей обычного качества.

Вероятность этих гипотез до опыта:

В результате опыта наблюдено событие А — прибор безотказно работал время t.

Условные вероятности этого события при гипотезах Н 1 и Н 2 равны:

Находим вероятность гипотезы Н 1 после опыта:

вероятность среднеквадратический дисперсия математический

Математическая статистика

Условие: Составить закон распределения дискретной случайной величины Х , вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.

Охотник стреляет по дичи до попадания, но может сделать не более трех выстрелов. Вероятность попадания при каждом выстреле равна 0,6. Составить закон распределения случайной величины Х — числа выстрелов сделанных стрелком. Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.

Решение: Вероятность того, что число промахов равно 0, равна 0,6

• — вероятность того, что число промахов равно 1, равна 0,4 ·0,6 =0,24 (в первом не попал, во втором попал)
• — вероятность того, что число промахов равно 2, равна 0,4·0,4·0,6=0,096 (в двух первых не попал, в третьем попал)
• — вероятность того, что число промахов равно 3, равна 0,4 ·0,4 ·0,4 =0,064 (в трёх первых не попал)

Математическое ожидание равно 0·0,6+1·0,24+2·0,096+3·0,064 = 0,624

Условие: Случайная величина Х задана функцией распределения F(X) .

Одним из важнейших понятий теории вероятностей является понятие случайной величины .

Случайной называют величину , принимающую в результате испытаний те или иные возможные значения, наперед неизвестные и зависящие от случайных причин, которые заранее не могут быть учтены.

Случайные величины обозначаются заглавными буквами латинского алфавита X , Y , Z и т. д. или заглавными буквами латинского алфавита с правым нижним индексом , а значения, которые могут принимать случайные величины — соответствующими малыми буквами латинского алфавита x , y , z и т. д.

Понятие случайной величины тесно связано с понятием случайного события. Связь со случайным событием заключается в том, что принятие случайной величиной некоторого числового значения есть случайное событие, характеризуемое вероятностью .

На практике встречаются два основных типа случайных величин:

1. Дискретные случайные величины;

2. Непрерывные случайные величины.

Случайной величиной называется числовая функция от случайных событий.

Например, случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента.

Дискретными случайными величинами называются случайные величины, принимающие только отдаленные друг от друга значения, которые можно заранее перечислить.

Закон распределения (функция распределения и ряд распределения или плотность вероятности) полностью описывают поведение случайной величины. Но в ряде задач достаточно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный вопрос. Рассмотрим основные числовые характеристики дискретных случайных величин.

Законом распределения дискретной случайной величины называется всякое соотношение , устанавливающее связь между возможными значениями случайной величиныи соответствующими им вероятностями .

Закон распределения случайной величины может быть представлен в виде таблицы :

Сумма вероятностей всех возможных значений случайной величины равна единице, т. е. .

Закон распределения можно изобразить графически : по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат — вероятности этих значений; полученные точки соединяют отрезками. Построенная ломаная называется многоугольником распределения .

Пример . Охотник, имеющий 4 патрона, стреляет по дичи до первого попадания или расходования всех патронов. Вероятность попадания при первом выстреле равна 0,7, при каждом следующем выстреле уменьшается на 0,1. Составить закон распределения числа патронов, израсходованных охотником.

Решение. Так как охотник, имея 4 патрона, может сделать четыре выстрела, то случайная величина X — число патронов, израсходованных охотником, может принимать значения 1, 2, 3, 4. Для нахождения соответствующих им вероятностей введем события:

— “попадание при i — ом выстреле”, ;

— “промах при i — ом выстреле”, причем события и — попарно независимы.

Согласно условию задачи имеем:

,

По теореме умножения для независимых событий и теореме сложения для несовместных событий, находим:

(охотник попал в цель с первого выстрела);

(охотник попал в цель со второго выстрела);

(охотник попал в цель с третьего выстрела);

(охотник попал в цель с четвертого выстрела либо промахнулся все четыре раза).

Таким образом, закон распределения случайной величины X имеет вид:

0,7

0,18

0,06

0,06

Пример. Рабочий обслуживает три станка. Вероятность того, что в течение часа первый станок не потребует регулировки — 0,9, второй — 0,8, третий — 0,7. Составить закон распределения числа станков, которые в течение часа потребуют регулировки.

Решение. Случайная величина X — число станков, которые в течение часа потребуют регулировки, может принимать значения 0,1, 2, 3. Для нахождения соответствующих им вероятностей введем события:

— “i — ый станок в течение часа потребует регулировки”, ;

— “i — ый станок в течение часа не потребует регулировки”, .

По условию задачи имеем:

, .

Условия скачивания работ (лицензионное соглашение).
Работы с данного сайта предназначены исключительно для ознакомления. Все права в отношении работы принадлежат ее законному правообладателю. Оплата доступа не предполагает продажу работы или прав на неё. Мы оказываем услуги подбора и систематизации информации. Сайт не несет ответственности за правильность теоретической и (или) практической частей в работе. Ответственность за неправомерное и незаконное использование работы лежит на пользователе. Полное или частичное воспроизведение и распространение учебных материалов сайта запрещено. Услуга предоставляется «как есть» («as is») и в том виде, в котором она доступна на момент предоставления, при этом никаких гарантий прямых или косвенных, не предоставляется (включая, но не ограничиваясь, гарантии по использованию Услуги в конкретных целях). Копирование материалов с сайта запрещено.
Политика конфиденциальности: Мы высоко ценим Ваш интерес к нашему проекту. Защита персональных данных для нас очень важна. Мы соблюдаем правила защиты персональных данных и защиты ваших данных от несанкционированного доступа третьих лиц (защита персональных данных).
Заполнение формы с контактными данными означает безоговорочное согласие с настоящей Политикой конфиденциальности и указанными в ней условиями обработки персональной информации.
Ниже приводится информация об обработке персональных данных.
1. Персональные данные. Цель сбора и обработки персональных данных.
1.1. Вы всегда можете посетить данную страницу, не раскрывая никакой персональной информации.
1.2. Под персональными данными понимается любая информация, относящаяся к определенному или определяемому на основании такой информации физическому лицу.
1.3. Мы собираем и используем персональные данные, необходимые для выполнения Вашего запроса, это – фамилия, имя, телефон и электронный адрес.
1.4. Мы не проверяем достоверность персональных данных, предоставляемых физическими лицами, и не проверяет их дееспособность.
2. Условия обработки персональной информации покупателя и её передачи третьим лицам.
2.1. При обработке персональных данных посетителей сайта мы руководствуется Федеральным законом РФ «О персональных данных».
2.2. В отношении персональной информации покупателя сохраняется ее конфиденциальность.
2.3. Мы не передаем персональные данные третьим лицам.
3. Меры, применяемые для защиты персональной информации пользователей.
Мы принимаем необходимые и достаточные организационные и технические меры для защиты персональной информации пользователя от неправомерного или случайного доступа, уничтожения, изменения, блокирования, копирования, распространения, а также от иных неправомерных действий с ней третьих лиц.
ИП Сатаев Тимур Сагитович ОГРН 311028003900327